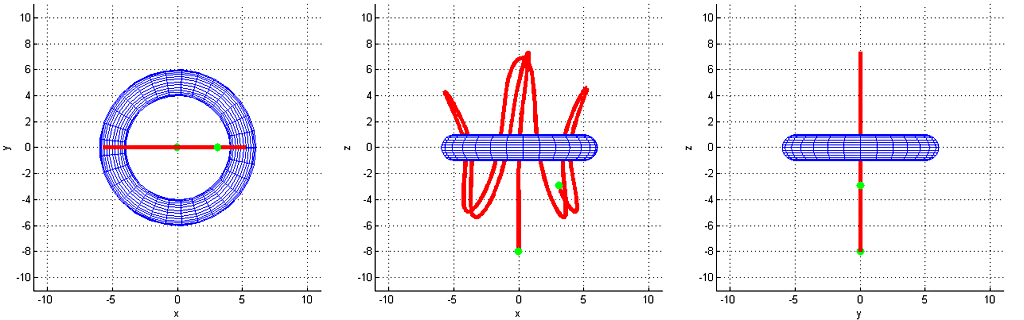
There are many games with a strong emphasis on gravity, and at times even multi-body trajectory simulations. However they all seem to be based on spherical geometry (as planets are shaped by gravity), but other shapes should create interesting trajectories. As torus has rotational symmetry its gravity field can be modelled on a 2D cross-section. In this project torus' field is estimated in 3D, projected to 2D and interpolation functions are fitted. The space- and time-efficient model could be used in a game to do physics simulation in real time.
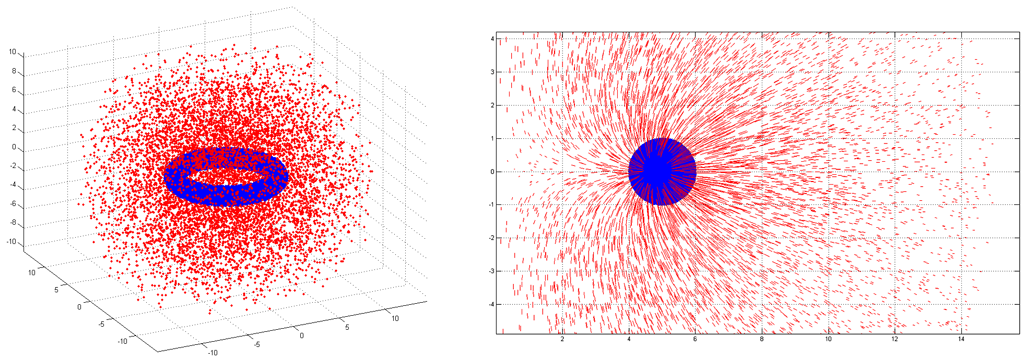
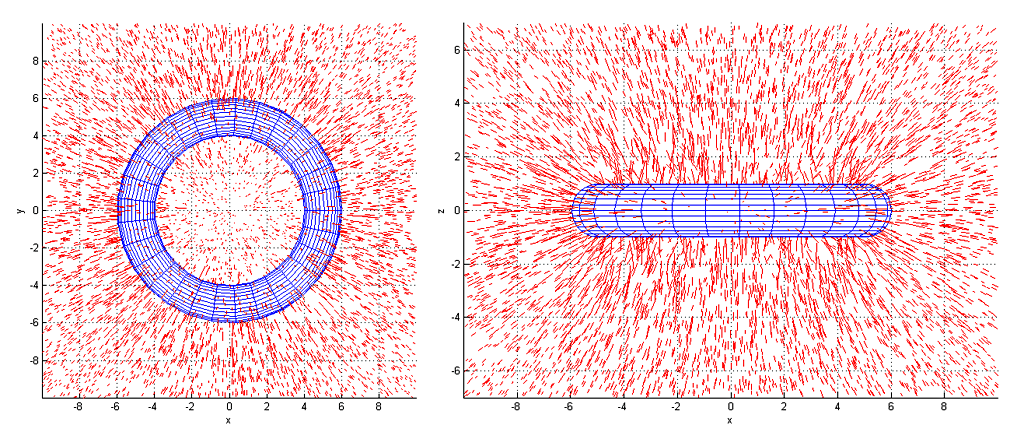
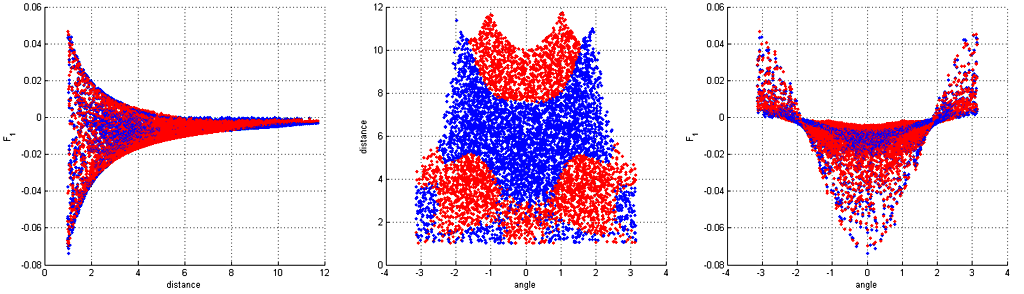
Instead of using numerical integration this simpler method was used as I wasn't sure I wouldn't introduce unintended biases when defining the integral over the volume of a torus. The process starts from generating random points within the torus (shown as blue in Figure 1) and outside it (shown in red). For each point outside the torus the gravitational field's force vector is estimated. These are then projected to a 2D cross-section, as shown on the right side of Figure 1. 3D plots of fields are shown in Figure 2. It can be seen to decay towards zero (as expected) at greater distances, but interestingly field goes to zero also at the origin due to the symmetry.
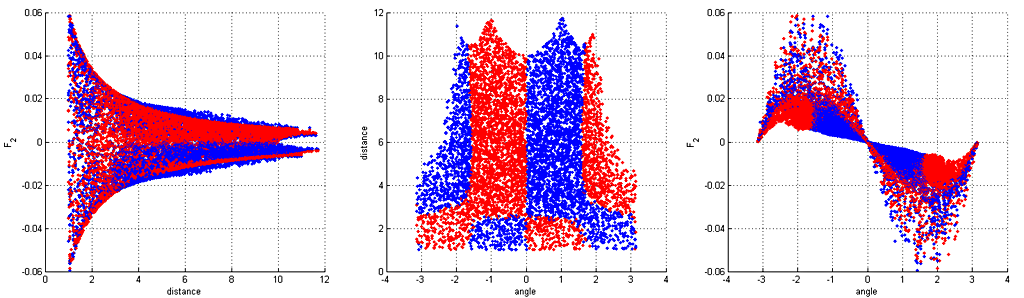
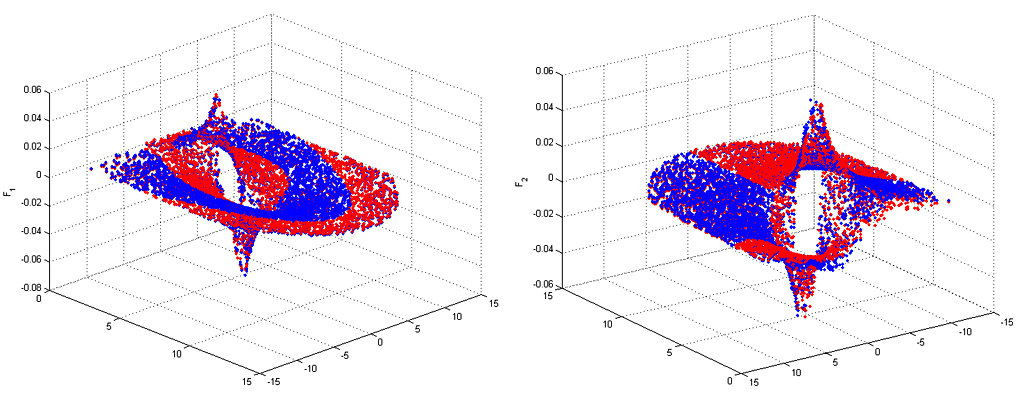
After 3D coordinates have been rotated to the 2D cross-section plane, coordinates are transformed log-polar coordinates. These are shown in Figure 3 (forces along x-axis) and Figure 4 (forces along y-axis). Their cartesian-coordinate counter-parts are shown in Figure 5. Shape of these graphs is a bit more apparent if they were seen in a rotating 3D animation. Red dots are correct values and blue values are forecasted by the fitted interpolation model. There is some residual error but it shouldn't be apparent in a game-like simulation.
The model for the force along axises have the following forms:
- Fx(α, d; p) → (p1cos(α)+
p2cos(2α)+p3) · exp(p4 · dp6) + p5
d + p7(1)
- Fy(α, d; p) → (p1sin(α) +
p2sin(3α)) · exp(p3 · dp4 + p5cos(α) +
p6cos(2α))(2)
Values for p at these two functions have the following values:
- Fx: [-2.1924 0.1201 -0.3083 -3.6119 5.4967e-04 0.2802 -0.0073]
- Fy: [-15.0000 -1.4790 0.1457 -5.5883 -0.2798 -0.1553]
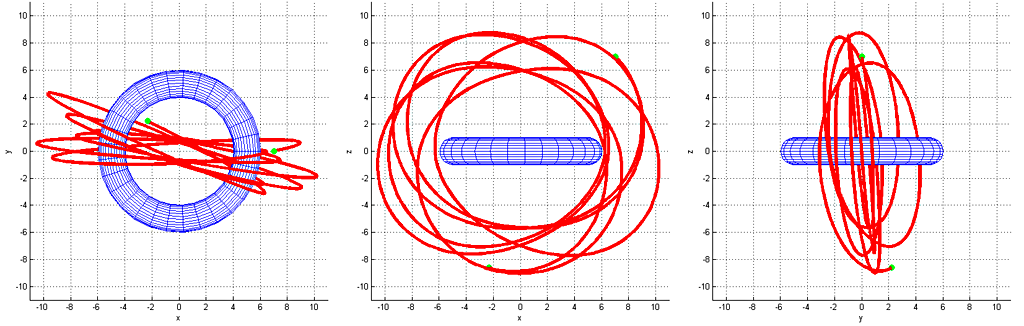
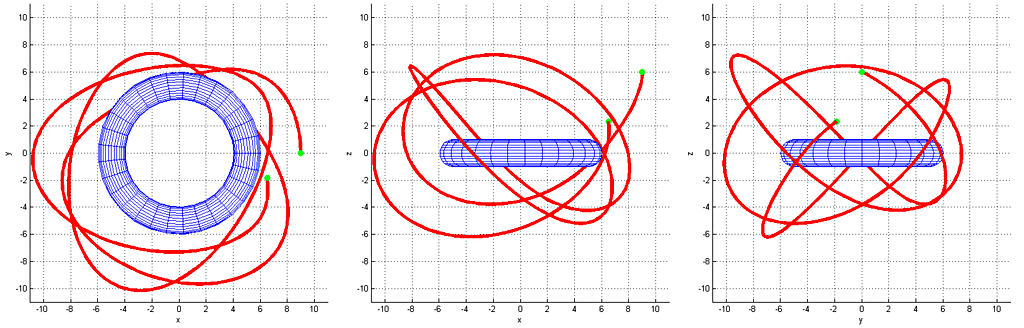
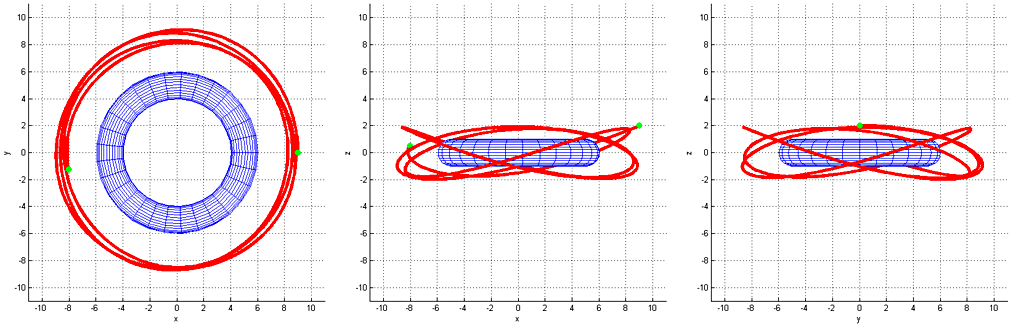
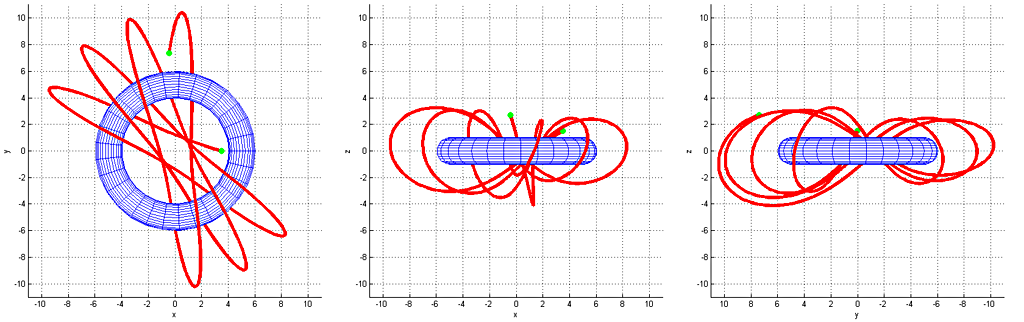
This geometry creates a field which have some interesting properties, when compared to the "standard" inverse square law (1/r2) of a spherical planet or a star. Four examples of these are shown in figures 6 - 10. There seems to exist various classes of non-closed trajectories as one could say torus has two degrees of "freedom" instead of just the one on spheres. I was happy to discover that there exists orbits which go through the hole in the middle (figures 9 and 10).
Trajectories were estimated by running the differential equation through the standard midpoint method with a suitably small time-step. Most trajectories seem to be fairly chaotic and unstable, so simulating additional bodies such as moons might have non-interesting results. It would be interesting to simulate an atmosphere consisting of ideal gas but I have no prior experience on that even on a spherical body. It would also be worth studying game-mechanics on the FPS genre, and why not also for a platformer?
Related blog posts:
|
|
|
|
|
|
|
|
|
|