Niko's Project Corner

Some peo­ple en­joy solv­ing puz­zles in the old fash­ioned way, but en­gi­neers would like to au­to­mate te­dious tasks like that. This is a well-suited task for su­per­vised learn­ing, but nat­urally it re­quires train­ing data. Gath­er­ing it from real-life puz­zles would be time-con­sum­ing as well, so I opted for gen­er­at­ing it in­stead. This gives a lot of con­trol on the data, but the re­sult­ing sys­tem might not even work with real-life in­puts. There are also sev­eral dif­fer­ent styles of puz­zles, but in this pro­ject each "base-piece" is a rect­an­gle of iden­ti­cal size. An ex­am­ple 3 × 3 puz­zle is shown in the thumb­nail.

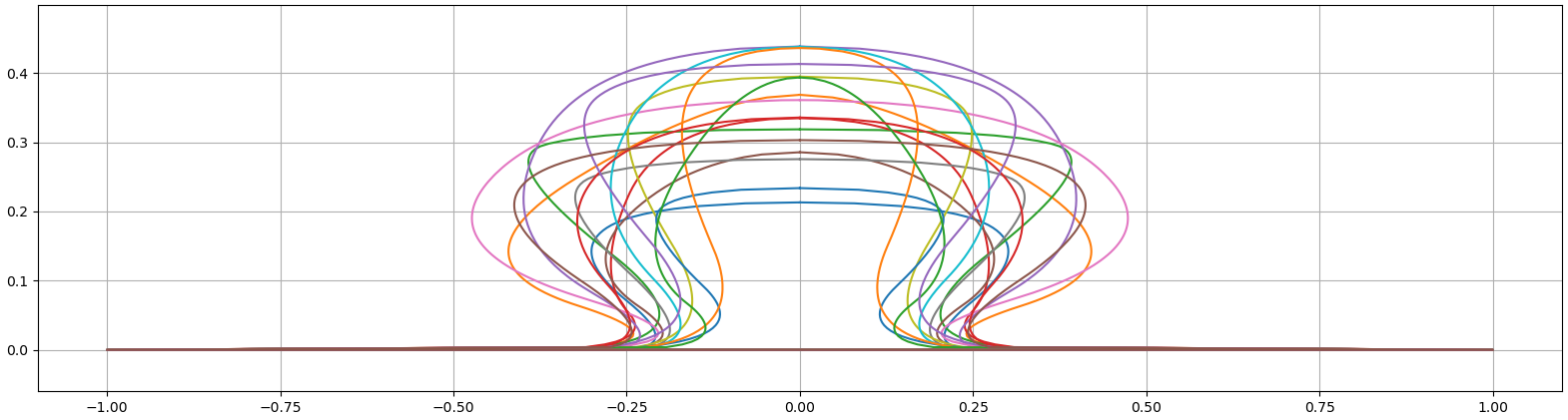
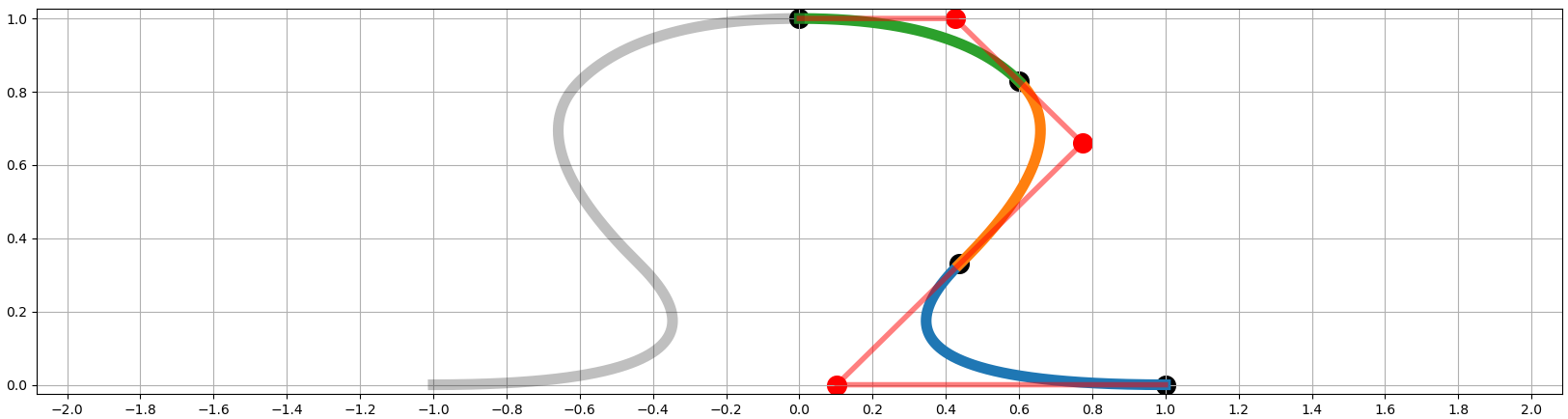
A "nor­mal­ized" puz­zle edge is de­fined as a set of Bezier curves, and is con­strained to al­ways start from co­or­di­nates (0,1) and to end to (1, 0). In ad­di­tion its slope is 100% hor­izon­tal at the be­gin­ning and at the end. This leaves them with four de­grees of free­dom. The curve con­sists of three Bezier curves, which are shown in dif­fer­ent col­ors in Fig­ure 1. They are spec­ified by three con­trol points, which are shown red. Black dots are ei­ther hard-coded be­gin­ning and end­ing co­or­di­nates, or in­ter­po­lated as the mid­point be­tween two red con­trol points. For sim­plic­ity this code gen­er­ates only sym­met­ri­cal edges, but nat­urally it could be ex­tended to more com­plex and asym­met­ric shapes.

Figure 1: A "nor­mal­ized" edge piece has four de­grees of free­dom, and it con­sists of three Bezier curves. When stitched to­gether like this, they form a sin­gle con­tin­uous path.

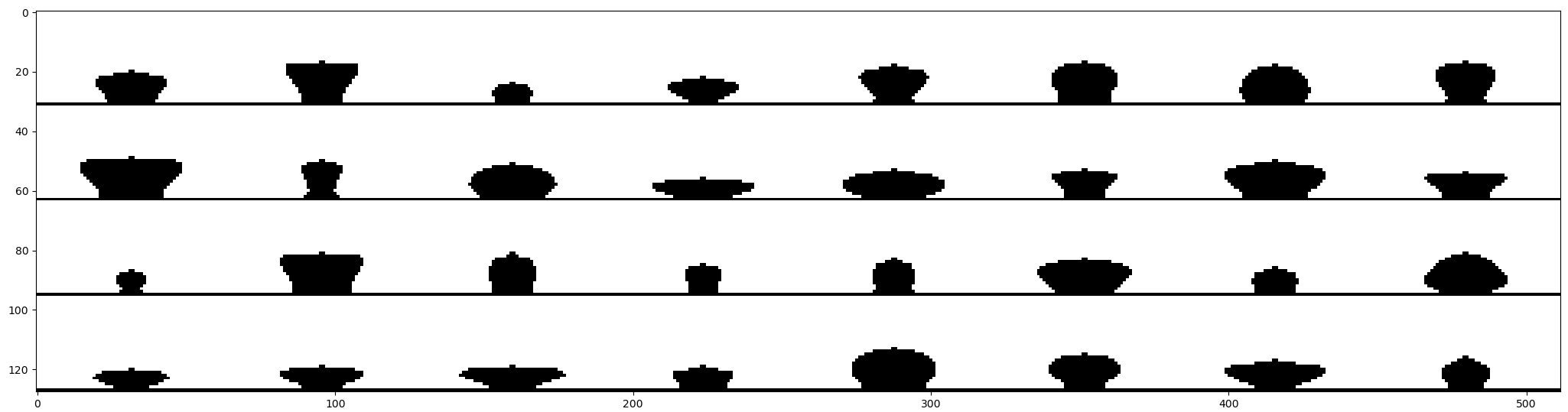
In ad­di­tion to the four "ba­sic" de­grees of free­dom, each shape can also be scaled along the x and y axis, so there are ac­tu­ally six pa­ram­eters to ad­just. Ran­domly sam­pled curves in Fig­ure 2 show the ex­tend of va­ri­ety in edges. Ras­ter­ized low-res­olu­tion ex­am­ples are shown in Fig­ure 3.

Figure 2: Ex­am­ples of ran­dom edge shapes, show­cas­ing all six de­grees of free­dom.

Figure 3: Ras­ter­ized ex­am­ples of ran­dom piece edges.

The amount of vari­ation within pix­els is vi­su­al­ized in Fig­ure 4. Im­ages' top cor­ners are al­ways white and the bot­tom mid­dle pixel is al­ways black, and on av­er­age the mid­dle area is be­tween these two ex­tremes. Var­ious gen­er­ated full puz­zle pieces are shown in Fig­ure 5. Ac­tu­ally each piece matches the neigh­bor­ing four other pieces, so the puz­zle is in a solved state. In ad­di­tion to choos­ing a ran­dom edge shape to each four sides, there is also an op­tion whether the piece has a "male" or "fe­male" part of the shape. A more de­tailed view of the pieces is shown in Fi­ugre 6.

Figure 4: Edge pixel's vari­ance is largest on the re­gion which has a 50% chance of be­ing ei­ther black or white. Many pix­els have a vari­ance of zero.

Figure 5: An ex­am­ple ran­dom puz­zle, only the top left cor­ner is shown.

Figure 6: A more zoomed in view of gen­er­ated pieces, from the top left cor­ner of the puz­zle.

The net­work con­sists of two parts: a shared fea­ture ex­trac­tion step us­ing 2D con­vo­lu­tions, and a fully con­nected de­ci­sion-mak­ing step. This ar­chi­tec­ture is com­monly known as a Siamese neu­ral net­work. The fea­ture ex­trac­tion com­presses the in­put im­age of size 64 × 64 × 1 to an out­put of 12 × 12 × 8, hav­ing 1152 el­ements. All ac­ti­va­tions here are re­lus. This ten­sor is then flat­tened, and a lin­ear layer pro­jects it down to just 64 di­men­sions. This fi­nal out­put size is a freely ad­justible hy­per­pa­ram­eter. A smaller num­ber of out­puts is less prone for over­fit­ting, but nat­urally at some point the model will only un­der­fit to the data. Fea­ture ex­trac­tion steps' ten­sor di­men­sions and the num­ber of layer pa­ram­eters is listed be­low.

• Layer (type) Output Shape Param #
• =================================================================
• (None, 64, 64, 1) 0
• conv2d_338 (Conv2D) (None, 62, 62, 16) 160
• batch_normalization_1049 (Ba (None, 62, 62, 16) 64
• conv2d_339 (Conv2D) (None, 60, 60, 32) 4640
• batch_normalization_1050 (Ba (None, 60, 60, 32) 128
• max_pooling2d (MaxPooling2D) (None, 30, 30, 32) 0
• conv2d_340 (Conv2D) (None, 28, 28, 64) 18496
• batch_normalization_1051 (Ba (None, 28, 28, 64) 256
• conv2d_341 (Conv2D) (None, 26, 26, 64) 36928
• batch_normalization_1052 (Ba (None, 26, 26, 64) 256
• max_pooling2d_1 (MaxPooling2 (None, 13, 13, 64) 0
• conv2d_342 (Conv2D) (None, 12, 12, 8) 2056
• flatten_163 (Flatten) (None, 1152) 0
• dense_5 (Dense) (None, 64) 73728
• =================================================================
• Total params: 136,744
• Trainable params: 136,376
• Non-trainable params: 368

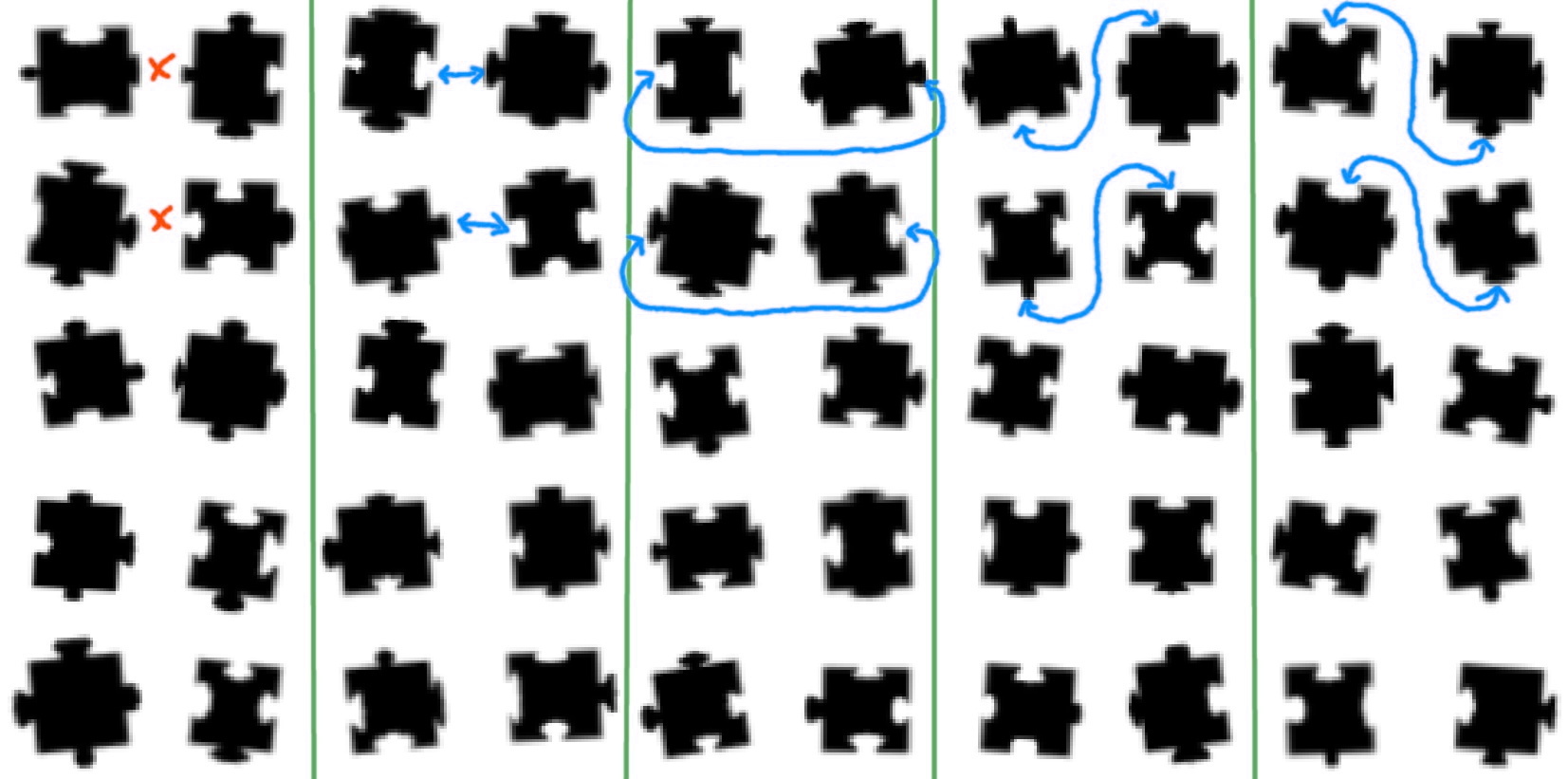
The "de­ci­sion" net­work is trained to pre­dict one of the five cases from two in­put pieces: ei­ther the pieces do not match, or they match right-to-left, left-to-right, bot­tom-to-top or top-to-bot­tom. Ex­am­ples of these are shown in Fig­ure 7. This means that the net­work doesn't need to con­sider whether to ro­tate one or both of the pieces by 90, 180 or 270 de­grees. It was as­sumed that this makes the net­work eas­ier to train and less prone to over­fit­ting. If also ro­ta­tions were taken into ac­count, the net­work would need 17 out­puts: one for a mis­match and 16 for each of the ways the four edges from piece A can be paired with the edges of piece B. In this so­lu­tion each piece pair has to be fed to the net­work four times. Piece A is used as-is, but the piece B has its im­age ro­tated by 0, 90, 180 and 270 de­grees. Since soft­max nor­mal­iza­tion is ap­plied sep­arately for each of the in­puts, the con­cate­nated out­put doesn't add up to 100%. Hope­fully the net­works' out­put is "con­sis­tent", mean­ing that it doesn't claim that the pieces fit to­gether in two dif­fer­ent ways. This hasn't been checked in the cur­rent pro­to­type.

Figure 7: Ex­am­ple in­put im­age pairs from the five dis­tinct classes: no match (left) or one pair of the four edges match with­out hav­ing to ro­tate ei­ther piece. The im­age also shows that the in­put res­olu­tion is rather small (64 pix­els), caus­ing some of the de­tails be lost. In­put im­ages are aug­mented with ran­dom zoom, trans­la­tion and ro­ta­tion to midi­gate over­fit­ting and hav­ing the net­work to be tol­er­ant of such er­rors in the in­put im­ages.

The de­ci­sion net­work's ten­sor sizes and the num­ber of layer pa­ram­eters is shown be­low. 136744 (96.4%) of the pa­ram­eters come from the fea­ture ex­trac­tion step. The net­work achieves an ac­cu­racy of about 97%.

• Layer (type) Output Shape Param #
• =================================================================
• (None, 64, 64, 2) 0
• model_1 (Functional) (None, 64, 2) 136744
• flatten_2 (Flatten) (None, 128) 0
• dense_7 (Dense) (None, 32) 4128
• batch_normalization_1089 (Ba (None, 32) 128
• dense_1240 (Dense) (None, 16) 528
• batch_normalization_1090 (Ba (None, 16) 64
• dense_1241 (Dense) (None, 8) 136
• batch_normalization_1091 (Ba (None, 8) 32
• dense_1242 (Dense) (None, 5) 45
• =================================================================
• Total params: 141,805
• Trainable params: 141,325
• Non-trainable params: 480

The fully im­ple­mented sys­tem would re­ceive a photo of an un­solved puz­zle, de­tect its pieces, ro­tate them into "or­thog­onal" north-south & east-west ori­en­ta­tion, feed each pair to the net­work and solve which pairs of pieces be­long to­gether. This might take sig­nif­icant amount of time, since even a small-ish puz­zle of 500 pieces has about 125k pairs to be checked, and re­mem­ber that each pair has to be run through the net­work four times (the other part is ro­tated in 90 de­gree in­cre­ments). How­ever this can be op­ti­mized by run­ning the net­work in two sep­arate steps: fea­ture ex­trac­tion and de­ci­sion mak­ing. One only needs to run the fea­ture ex­trac­tion for 500 × 4 im­ages, and this ac­counts for al­most 100% of the cal­cu­la­tion re­quire­ments. The de­ci­sion step is very light weight, con­sist­ing only of a se­quence of dense lay­ers with small in­puts.

The last step would be to in­spect the pre­dicted puz­zle piece matches, and con­struct the most likely glob­ally con­sis­tent so­lu­tion to the puz­zle. If the false pos­itive rate isn't too high, there aren't that many plau­si­ble so­lu­tions. Puz­zle con­stru­cion is nat­urally very tol­er­ant of false neg­atives, since it is suf­fi­cient that the piece is cor­rectly matched to two or three of its four neigh­bor­ing pieces.

Related blog posts:

Cheating at Bananagrams with real-time AI, part 1, 2023 Apr (Matching: Computer Vision, Keras, Python)
Image and video clustering with an autoencoder, 2022 Jan (Matching: Computer Vision, Keras, Python)
Helsinki Deblur Challenge 2021, 2021 Dec (Matching: Computer Vision, Keras, Python)
Chess video search engine, 2021 Jun (Matching: Computer Vision, Keras, Python)
Introduction to Stable Diffusion's parameters, 2022 Nov (Matching: Computer Vision, Python)