Niko's Project Corner

Bruteforcing Countdown numbers game with CUDA

Youtu­ber An­other Roof posed an in­ter­est­ing ques­tion on his video "The Sur­pris­ing Maths of Britain's Old­est* Game Show". The chal­lenge was stated in the video's de­scrip­tion: "I want to see a list of the per­cent­age of solv­able games for ALL op­tions of large num­bers. Like I did for the 15 op­tions of the form {n, n+25, n+50, n+75}, but for all of them. The op­tions for large num­bers should be four dis­tinct num­bers in the range from 11 to 100. As I said there are 2555190 such op­tions so this will re­quire a clever bit of code, but I think it’s pos­si­ble!". His ref­er­ence Python im­ple­men­ta­tion would have taken 1055 days (25000 hours) of CPU time (when all four large num­bers are used in the game), but with CUDA and a RTX 4080 card it could be solved in just 0.8 hours, or 31000x faster!

Satellite crash course

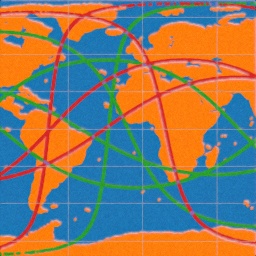
Since hear­ing the news of a fal­ing Chi­nese rocket booster Long March 5B and be­ing re­minded that Earth's sur­face is about 70% ocean, I got in­ter­ested on how the or­bital pa­ram­eters af­fect the odds of crash­ing to ocean vs. ground. I was nearly fin­ished with the pro­ject when I re­al­ized that Earth is ro­tat­ing un­der the satel­lite, thus in­val­idat­ing all the re­sults! This doesn't take or­bits' ec­cen­tric­ity into ac­count ei­ther, but I've heard that the ath­mo­spheric drag has a den­dency of re­duc­ing it to zero as the or­bit falls. Any­way, I found the var­ious "straight" paths around the globe in­ter­est­ing and de­cided to pub­lish these re­sults any­way. In con­clu­sion there are paths which spend only 9 % on top of land (in­clud­ing lakes) and 91% on top of ocean or up-to 57% on top of land and 43% on top of ocean.

Simulating gravitational field near a torus

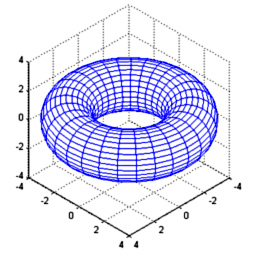
There are many games with a strong em­pha­sis on grav­ity, and at times even multi-body tra­jec­tory sim­ula­tions. How­ever they all seem to be based on spher­ical ge­om­etry (as plan­ets are shaped by grav­ity), but other shapes should cre­ate in­ter­est­ing tra­jec­to­ries. As torus has ro­ta­tional sym­me­try its grav­ity field can be mod­elled on a 2D cross-sec­tion. In this pro­ject torus' field is es­ti­mated in 3D, pro­jected to 2D and in­ter­po­la­tion func­tions are fit­ted. The space- and time-ef­fi­cient model could be used in a game to do physics sim­ula­tion in real time.

Approximating planets' orbits in closed-form

I wanted to find or cre­ate a for­mula which would ac­cept an epoch times­tamp, lat­itude and lon­gi­tude and it would pro­duce the Sun's ob­served az­imuth and al­ti­tude in ra­di­ans. It needs to take into ac­count de­tails earth's ax­ial tilt and its po­si­tion on its or­bit around the sun. To my sur­prise I wasn't able to find such for­mula, so I had to de­velop it from scratch. Luck­ily earth's or­bit (and or­bits in gen­eral) is a well stud­ied and doc­umented prob­lem, so I could take some short­cuts.