Niko's Project Corner

Nowa­days there are many HTML5-based map ser­vices, but typ­ically they don't of­fer any ex­port func­tion­al­ity. To cre­ate a full view of the de­sired re­gion, one can ei­ther zoom out (and lose map de­tails) or take many screen­shots of dif­fer­ent lo­ca­tions and man­ually stitch them to­gether. This pro­ject can au­to­mat­ically load all stored screen­shots, de­tect the map, crop rel­evant re­gions, de­ter­mine im­ages rel­ative off­sets and gen­er­ate the high-res out­put with zero con­fig­ura­tion from any map ser­vice.

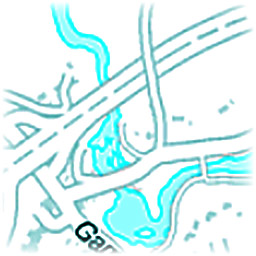
The first step is to de­ter­mine which re­gion of the im­age is the map and which parts should be ig­nored. This is achieved by as­sum­ing that the only mov­ing part of the page is the map it­self (no scrolling of the page, no ads, ...). Un­der these as­sump­tions it is triv­ial to cre­ate a mask sim­ilar to the one at Fig­ure 1. Rel­evant rows and columns (and thus the rect­an­gu­lar crop­ping re­gion) can be de­ter­mined based on it.

Figure 1: One of the in­put screen­shots on the left and the re­sult­ing change-mask on the right. Bright pix­els vary be­tween im­ages, and thus can be as­sumed to be part of the map.

Once map re­gions have been ex­tracted, their rel­ative po­si­tions need to be de­ter­mined be­fore stitch­ing is pos­si­ble. This is a spe­cial case of a panoramic im­age gen­er­ation, which is typ­ically solved by Fea­ture de­tec­tion and ro­bust RANSAC based match­ing pro­ce­dure. How­ever in this map case we only need to es­ti­mate the trans­la­tion in x- and y-di­rec­tions, and no ro­ta­tion or scal­ing should have oc­curred. We can also as­sume that the im­age i should have sig­nif­icant over­lap with im­ages i-1 and i+1, per­haps even with i-2 and i+2. Fourier trans­form base Phase cor­re­la­tion is a per­fect so­lu­tion this task, be­cause it isn't com­pu­ta­tion­ally too heavy, is very ro­bust, al­ways finds the "best" an­swer and is very easy to im­ple­ment. It is based on cal­cu­lat­ing 2D Fourier trans­forms G_a and G_b of im­ages a and b and cal­cu­lat­ing the in­verse Fourier trans­form F^-1((G_a · G_b^* ) / | G_a · G_b^* |) where element-wise multiplication is used. This should result in a single bright spot, and its mid-point indicates the translation which maximizes the pixel-wise correlation metric.

It is im­por­tant to ap­ply suf­fi­ciently large zero padding when Fourier trans­forms are be­ing cal­cu­lated. Oth­er­wise for an im­age of 1000 × 1000 res­olu­tion the move­ment of 500 pix­els up­wards looks sim­ilar to 500 pix­els down­wards, and this am­bi­gu­ity would need to be re­solved via other means.

If im­age i's lo­ca­tion is only cal­cu­lated rel­ative to i-1 and not to i-2, a sim­ple chain of po­si­tion con­strains is cre­ated which is suf­fi­cient to de­ter­mine each im­age's lo­ca­tion rel­ative to each other. If sig­nif­icant cor­re­la­tion was found also with i-2, then an over-con­strained lin­ear equa­tion sys­tem is con­structed, but it has an unique least squares so­lu­tion.

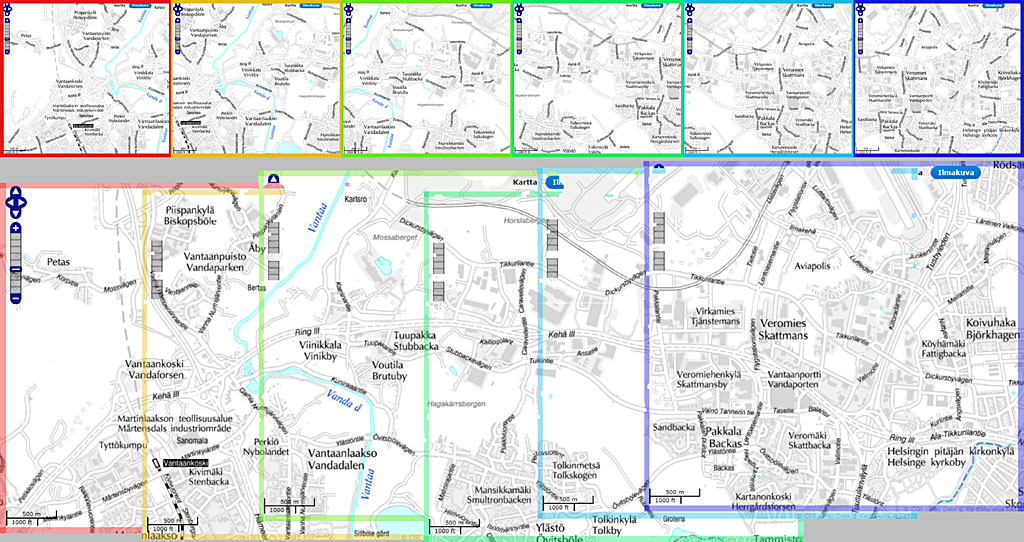
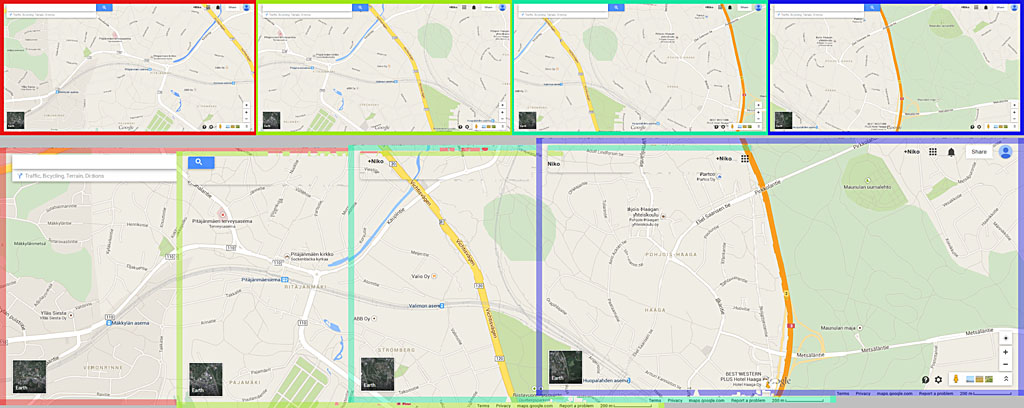
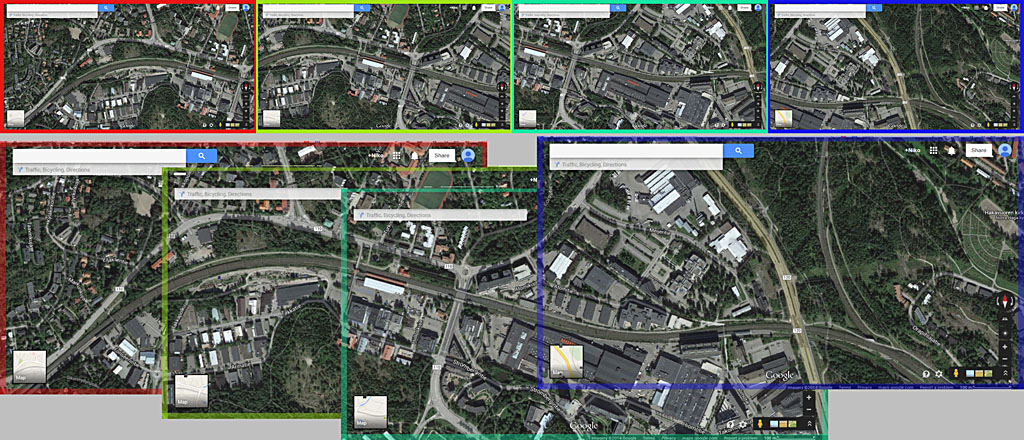
Once im­age po­si­tions have been de­ter­mined they need to be com­posed to­gether. They are pro­cessed se­quen­tially one-by-one, and the pixel vari­ation map (see Fig­ure 1) is used to pri­or­itize over­lap­ping pix­els. This re­moves UI el­ements such as nav­iga­tion from the fi­nal out­put when pos­si­ble. The al­go­rithm have been tested with var­ious screen­shot se­quences, but al­ways us­ing the same con­fig­ura­tion and thresh­olds. Re­sults can be seen in fig­ures 2 to 5, and they all worked out with­out any prob­lems. The im­age top shows in­di­vid­ual cap­tured maps and the bot­tom shows the ren­dered fi­nal out­put (with en­hanced im­age bor­ders for bet­ter vi­su­al­iza­tion).

Figure 2: Map parts and the fi­nal out­put from Re­it­tiopas.fi.

Figure 3: Map parts and the fi­nal out­put from GoThere.sg.

Figure 4: Map parts and the fi­nal out­put from Goole Maps (map view).

Figure 5: Map parts and the fi­nal out­put from Goole Maps (satel­lite view).

The only re­main­ing part would be to re-im­ple­ment all this in C++ (by uti­liz­ing FFTW and FastCGI again) and pub­lish it as a web ser­vice. Users would ei­ther use a browser plugin to cap­ture screen­shots or man­ually save them on the disk and up­load from there. This would be a fairly sim­ple sys­tem to do and host it on my home server, but it has a few prob­lems. One is the sys­tem sta­bil­ity, up­time and mon­itor­ing as­pect, be­cause if the FastCGI pro­cess crashes for any rea­son then the site would be ef­fec­tively down.

The other pos­si­ble prob­lem is the band­width and CPU us­age. Ei­ther al­most no­body uses the ser­vice which wouldn't be too mo­ti­vat­ing, or too many peo­ple would try to use it si­mul­ta­ne­ously and it would be too slow or un­sta­ble. I might do this one day, but now I'm al­ready hav­ing new pro­jects in mind.

Related blog posts:

Cheating at Bananagrams with real-time AI, part 1, 2023 Apr (Matching: Computer Vision)
Introduction to Stable Diffusion's parameters, 2022 Nov (Matching: Computer Vision)
Matching puzzle pieces together, 2022 Jul (Matching: Computer Vision)
Single channel speech / music separation, 2022 Feb (Matching: FFT)
Image and video clustering with an autoencoder, 2022 Jan (Matching: Computer Vision)