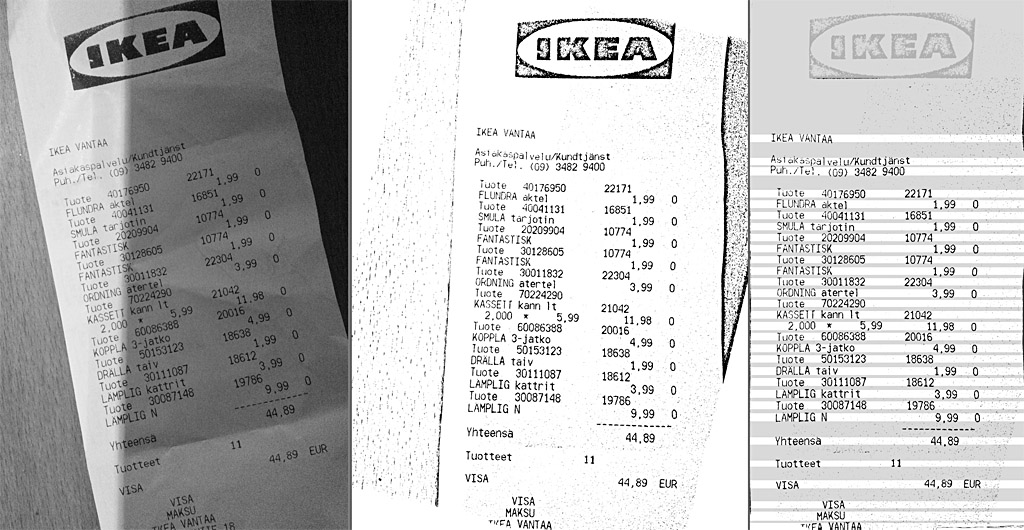
This project's goal was to automatically and robustly estimate and compensate distortion from any receipt photos. The user is able to just snap the photo and OCR could accurately identify bought products and their prices. However this task is somewhat challenging because typically receipts tend to get crumbled and bent. Thus they won't lie nicely flat on a surface for easy analysis. This set of algorithms solves that problem and produces distortion-free thresholded images for the next OCR step.
The first step is to convert the image to black & white and to adaptively threshold it to separate black letters from white-to-gray background. Typically the light comes from top so the used camera, phone or a tabled tends to cast a shadow on it. Hopefully its border will be at least slightly "smooth", so that it won't get mis-thresholded as actual ink on the receipt. I used this formula to compensate light and shadow effects from the image:
- I'x,y = Clamp[0, 1]( a + b
· log Ix,y⁄GaussBlurσ,x,y(I) )(1)
Basically each (x, y) location's brightness is compared to it surrounding brightness, which is determined by applying the standard Gaussian blur at chosen σ. Parameters a and b adjust the "blackness" range and the result is clamped to have values between 0.0 and 1.0.
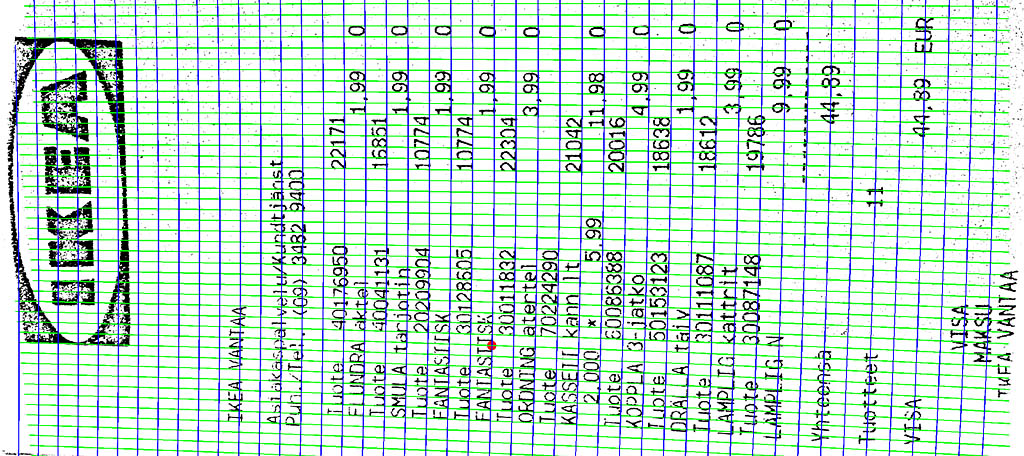
The resulting black pixels are separated to clusters based on their connectivity with neighbouring pixels. Clusters with 60 to 500 pixels are assumed to be individual characters. Each valid cluster's major and minor axises are determined by running the standard PCA algorithm and checking its major and minor singular values. Clusters with 75% of variance on the major direction and having a major singular value of at least 50 are accepted for orientation voting. These thresholds filter out spurious votes from too round or too small clusters. The outcome can be seen in Figure 1.

After the main rotation has been compensated, the next step is to estimate distortions caused by the perspective and/or bent receipt. It is accomplished by generating the Delaunay triangulation of observed characters and identifying strictly horizontal and vertical segments. And example result can be seen in Figure 2. These lines are used to robustly fit the following linear models for horizontal direction α, vertical direction β and the scale (S) at the location (x,y):
- α(x,y) = a1,x x + b1,y y +
c1(2)
- β(x,y) = a2,x x + b2,y y + c2(3)
- S(x,y) =
exp(a3,x x + b3,y y + c3)(4)
Since the main rotation has been compensated already, c1 and c2 should be approximately zero. The distortion is compensated by following the dynamic model for horizontal (ph) and vertical (pv) movement:
- ∂⁄∂x
ph(x,y) = cos(α(x,y)) · S(x,y)(5)
- ∂⁄∂y ph(x,y)
= sin(α(x,y)) · S(x,y)(6)
- ∂⁄∂x pv(x,y)
= -sin(β(x,y)) · S(x,y)(7)
- ∂⁄∂y pv(x,y)
= cos(β(x,y)) · S(x,y)(8)
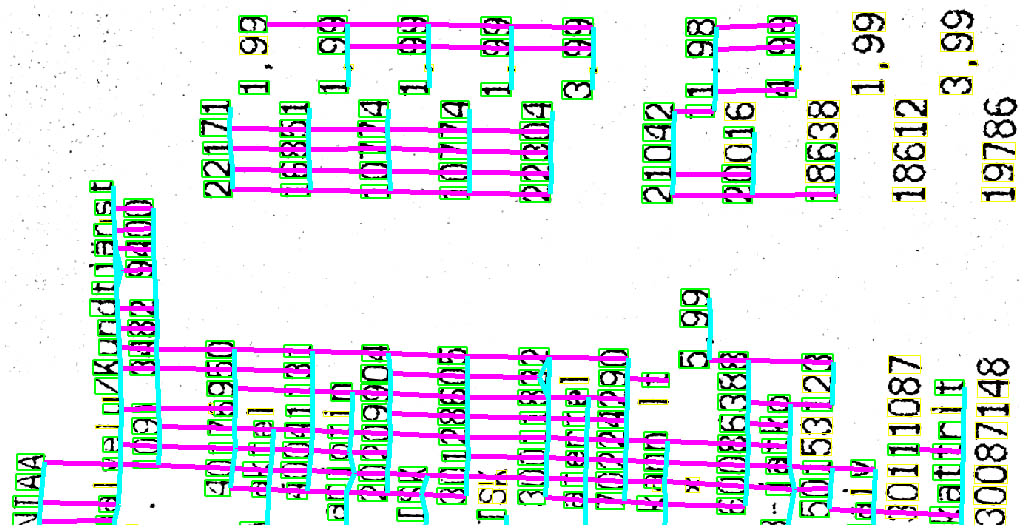
These can be used to construct an inverse mapping which straightens out remaining curvatures and scale changes. Its outcome is visualized at Figure 3, where it is apparent that vertical and horizontal lines align very well with the underlying monoface font.
The final step is to render the undistorted image and to do final receipt and text line detection. Receipt is horizontally cropped if significant black border separates it from the left and right parts of the image. Because distortions have been corrected already these lines should be fairly accurately purely vertical. Then text lines are detected and separated from others based on white horizontal rows between them. This output should be fairly easy for OCR algorithms to analyze.
Related blog posts:
|
|
|
|
|
|
|
|
|
|