Niko's Project Corner

My Mas­ters of Sci­ence The­sis in­volved the us­age of a so-called "om­ni­di­rec­tional cam­era". There are vari­ous ways of achiev­ing 180° or even 360° view, with their dis­tinct pros and cons. The gen­eral ben­efit of these al­ter­na­tive cam­era sys­tems is that ob­jects don't need to be tracked, be­cause gen­er­ally they stay with­ing the ex­tremely broad Field of View (FoV) of the cam­era. This is also very ben­efi­cial in vi­sual odom­etry tasks, be­cause land­marks can be tracked for longer pe­ri­ods of time.

Some de­sign op­tions are shown in Fig­ure 1. The sim­plest so­lu­tion is to use a fish-eye lens, and it is fairly straight for­ward to cal­ibrate. How­ever the im­age res­olu­tion is typ­ically some­what lim­ited, and it can­not cover much more than 180°. An al­ter­na­tive ap­proach is to use mul­ti­ple nor­mal cam­eras, an com­bine their im­ages in soft­ware. This can pro­duce very high res­olu­tion im­ages, but re­quires a lot more ef­fort and pa­ram­eters in cal­ibra­tion, es­pe­cially since also vinget­ting needs to be cor­rected be­fore im­ages can be joined seam­lessly to­gether. There are com­mer­cial prod­ucts such as La­dy­bug from Point­Grey. The third op­tion is to use a com­bi­na­tion of a tra­di­tional lens and a con­cave mir­ror to achieve up to 360° × 90° FoV. These are rel­atively com­pact and mid-priced, with a bit lim­ited res­olu­tion and a fairly sim­ple cal­ibra­tion mod­els and pro­ce­dures. This is the type of cam­era sys­tem I used at my Mas­ter's The­sis, which was ti­tled Real Time Fea­ture Track­ing on Om­ni­di­rec­tional Cam­era Im­age in Forest En­vi­ron­ment.

Figure 1: Al­ter­na­tive de­signs for om­ni­di­rec­tional cam­era sys­tem: a) fish-eye lens b) multi-cam­era rig c) cata­diop­tic sys­tem.

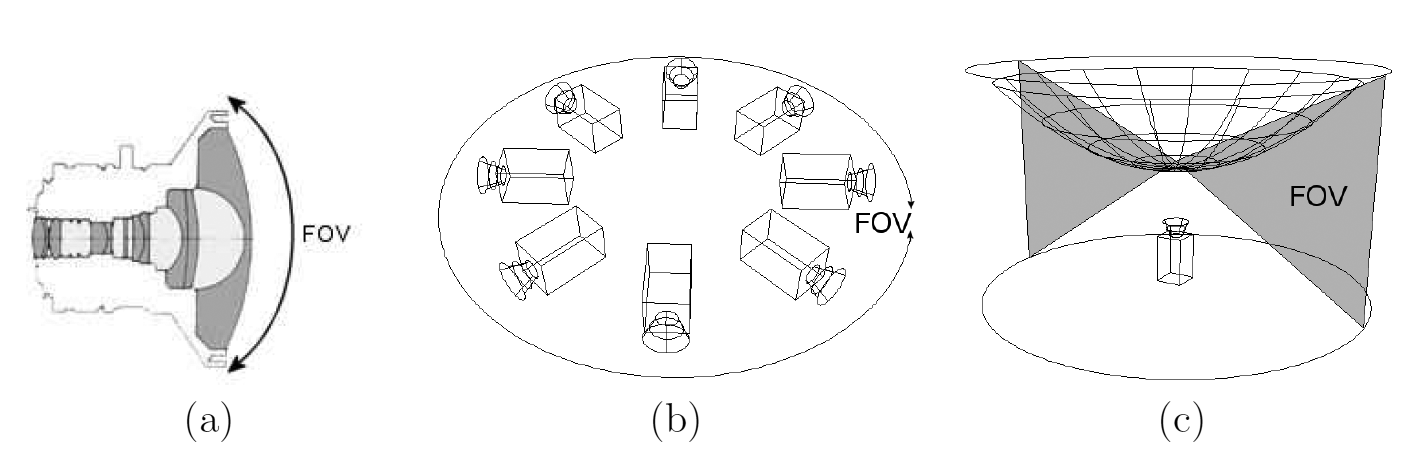
The cam­era sys­tem I used in my the­sis is pre­sented in Fig­ure 2. In ad­di­tion to the om­ni­di­rec­tional cam­era sys­tem, it has an In­er­tial Mea­sure­ment Unit (IMU) and a sup­port­ing struc­ture to at­tach an com­pact 2D laser scan­ner (40 × 40 mm) such as Hokuyo URG. This leaves us with a FoV of about 290°, which is not an prob­lem be­cause typ­ically part of FoV would be blocked by the user or robot any­way. Any­way this dark area can be ig­nored dur­ing im­age rec­ti­fi­ca­tion.

One in­tu­itive im­age rec­ti­fi­ca­tion model is to make each im­age pixel cor­re­spond to an equal solid an­gle. For ex­am­ple if the cam­era has a FoV of 360° × 90°, suit­able im­age res­olu­tions would have res­olu­tions such as 360 × 90 and 720 × 180. To de­ter­mine the ac­tual map­ping, the cam­era must be cal­ibrated.

Figure 2: A cata­diop­tric om­ni­di­rec­tional cam­era (con­sist­ing of a tra­di­tional lens and a hy­per­bolic mir­ror). It also has an In­er­tial Mea­sure­ment Unit (IMU) and a place for a 2D laser scan­ner.

An ex­am­ple cap­tured frame can be seen in Fig­ure 3. The cap­tured im­age on the right, and the con­verted panorama is on top-right. The bot­tom-right im­age is over­layed with in­ter­est points and their tracks, and some meta­data about the pro­gram's frame rate etc. This was gen­er­ated by the pro­gram I de­vel­oped for my Mas­ter's The­sis, which I'll de­scribe in an other ar­ti­cle.

Figure 3: An ex­am­ple om­ni­di­rec­tional frame, with equian­gu­lar panorama and tracked in­ter­est points.

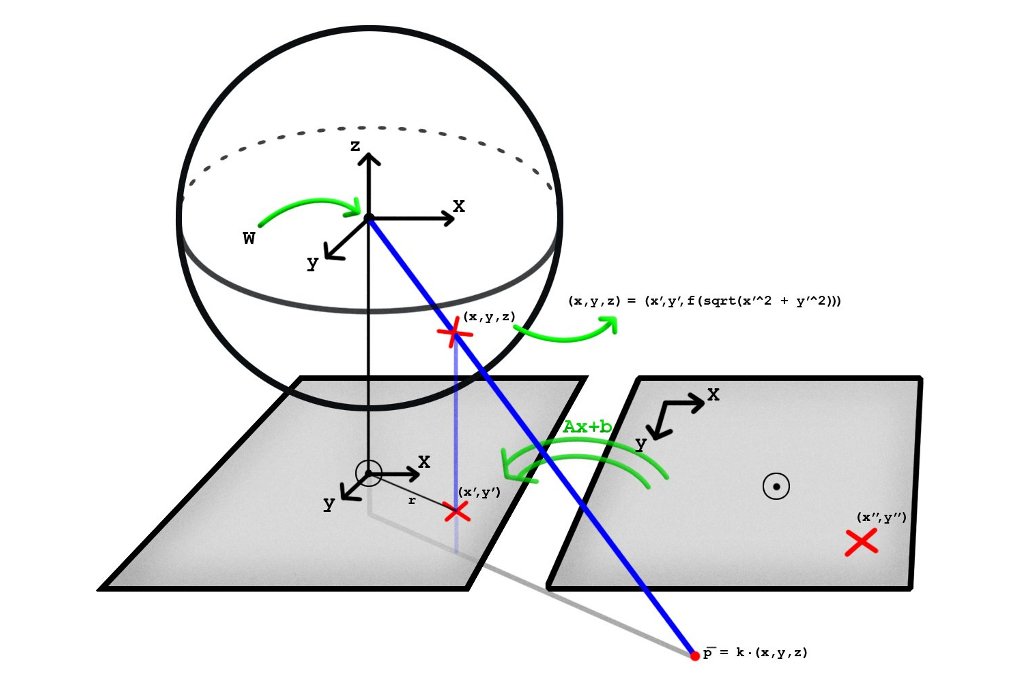
One sim­ple model was pre­sented in [1], which is based on a kind of an radial basis function to determine the z-component of the light ray (when camera is looking at the z-direction). This is illustrated in Figure 4, and other illustrations can be seen in the original paper. In this model it is very easy to determine the light ray's direction for each pixel, but it is more difficult to calculate the object's location on the image based on its position in relation to the camera.

Figure 4: Cam­era model for per­spec­tive and an om­ni­di­rec­tional cam­eras.

Let's first re­vise how the typ­ical per­spec­tive cam­era is parametrized. The lin­ear pin­hole cam­era model is well de­scribed in Wikipedia. It is im­por­tant to dif­fer­en­ti­ate be­tween in­trin­sic and ex­trin­sic pa­ram­eters. Ba­si­cally in­trin­sic pa­ram­eters de­scribe the phys­ical as­pects of the cam­era and lens, such as fo­cal length and pixel den­sity. Ex­trin­sic pa­ram­eters de­scribe the lo­ca­tion and ori­en­ta­tion of the cam­era in world co­or­di­nates. To de­ter­mine ob­ject's lo­ca­tion in the im­age, first ex­trin­sic pa­ram­eters are used to de­ter­mine ob­ject's lo­ca­tion in cam­era's co­or­di­nate sys­tem. Then in­trin­sic pa­ram­eters are used to pro­ject the ob­ject to the cam­era's sen­sor plane. To de­ter­mine that which di­rec­tion a given pixel is ob­serv­ing, these steps are ap­plied in re­verse or­der. This model can­not ac­count for lens dis­tor­tion, nor it mod­els vi­gnetting.

This same model can­not be ap­plied to om­ni­di­rec­tional cam­eras, be­cause it op­er­ates on a fun­da­men­tally dif­fer­ent prin­ci­ple. In­ter­est­ingly the more generic model can be used to de­scribe any cam­era with a sin­gle view­point prop­erty, in­clud­ing per­spec­tive cam­eras. For these it is also able to ac­count for lens dis­tor­tion.

Start­ing from a point on the im­age, it is first trans­formed via affine trans­for­ma­tion into a new co­or­di­nate sys­tem, in which the origin is close to the im­age cen­ter. This is es­sen­tially the same parametriza­tion as in the pin­hole cam­era model. Then the pixel's dis­tance from the new origin is de­ter­mined, and it is used to eval­uate a low-de­gree poly­no­mial func­tion to de­ter­mine the z-com­po­nent of the ray. Usu­ally the poly­no­mial needs to have a higher de­gree than two, but not re­ally greater than four.

If the cam­era is also able to see ''be­hind'' it, then this poly­no­mial will get also neg­ative val­ues. For an ideal pin­hole cam­era this func­tion would just have con­stant value, which cor­re­sponds to the fo­cal length of the lens (in pixel units). When lens dis­tor­tion is pre­sent, it will ei­ther grow (for bar­rel dis­tor­tion) or de­crease (for pin­cush­ion dis­tori­ton) as the pix­els are fur­ther away from the cen­ter. Nev­er­the­less for nor­mal lenses it will not de­vi­ate that much from its value at the origin. There can be greater changes for fisheye lenses.

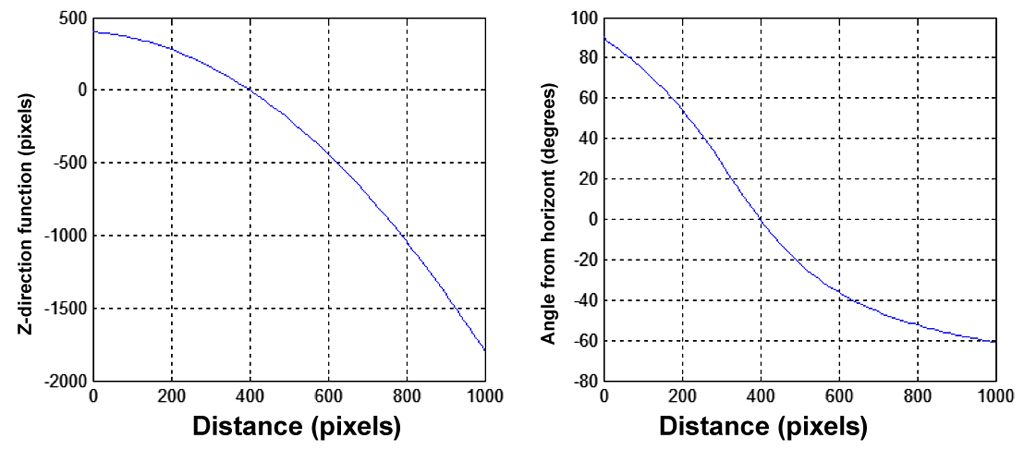
For the used om­ni­di­rec­tional sys­tem this func­tion started from a big pos­itive value, reached 0 at a dis­tance of \tex­tasci­itilde 500 pix­els and grows to pos­itive af­ter that. This means that pix­els near the im­age cen­ter are ac­tu­ally gath­er­ing light be­hind the cam­era, or in case the cam­era is pointed up­wards, these pix­els are see­ing the ground. Cor­re­spond­ingly pix­els near the im­age bor­der are gath­er­ing light above the hori­zon.

To use this cal­ibra­tion data for gen­er­at­ing a panoramic im­age in which each pixel cov­ers the equal solid an­gle, this map­ping func­tion needs to be used to de­ter­mine the az­imuth an­gle for each pixel dis­tance. This is cal­cu­lated as α(r) = arc­tan(^f(r)⁄_r), which clearly does not have a closed form so­lu­tion. The re­la­tion­ship be­tween f(r) and α(r) can be seen in Fig­ure 5 for f(r) = 400 - 0.2 r - 0.002 r².

Figure 5: An ex­am­ple poly­no­mial for an om­ni­di­rec­tional cam­era with a FoV of 360° × (90 + 60)° = 360° × 150°. It is ev­ident than be­cause f(400) = 0, then α(400) = 0°, in­di­cat­ing that these pix­els are ob­serv­ing light from the hor­izon­tal di­rec­tion.

To sam­ple im­ages from 65° to -40° at 15° in­ter­vals, the cor­re­spond­ing dis­tances from the im­age cen­ter are roughly 150, 220, 280, 330, 380, 440, 520 and 630 pix­els. The re­sult­ing pixel sam­pling pat­tern is shown in Fig­ure 6, with 24 sam­ples along the hor­izon­tal an­gle.

Figure 6: Ex­am­ple sam­pling pat­tern for gen­er­at­ing a panoramic im­age.

Related blog posts:

Cheating at Bananagrams with real-time AI, part 1, 2023 Apr (Matching: Computer Vision)
Introduction to Stable Diffusion's parameters, 2022 Nov (Matching: Computer Vision)
Matching puzzle pieces together, 2022 Jul (Matching: Computer Vision)
Image and video clustering with an autoencoder, 2022 Jan (Matching: Computer Vision)
Helsinki Deblur Challenge 2021, 2021 Dec (Matching: Computer Vision)