An interesting question was posted to crypto.stackexchange.com: "Is there a simple hash function that one can compute without a computer?" Here are three proposed algorithms based on Zobrist hashing, RC4 and A5/1. These should be reasonably secure even against attacks with a calculator, except the one based on Zobrist hashing (but I don't know how to prove or dis-prove this claim). These constructs are especially well suited for commitment schemes.
The first algorithm is based on Zobrist hashing, which is commonly used at chess engines and other similar applications to implement transposition tables. It is based on pre-generating random integers to a look-up table, and then selectively XORing them together to calculate a hash. This construct has tunable parameters which allow for a trade-off between security and the ease of computation.
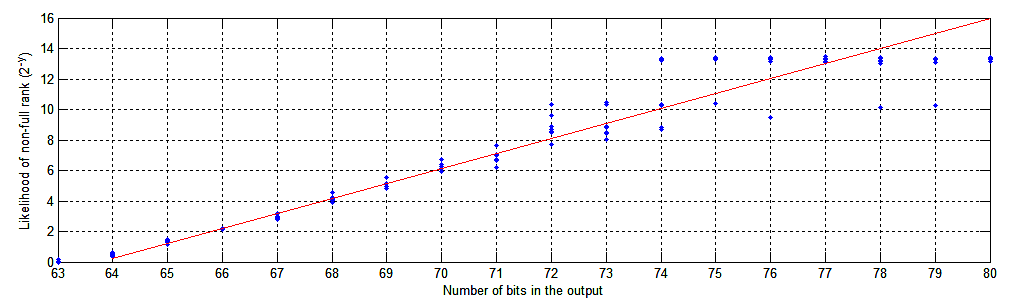
For relatively high security it is proposed to use 64 random 80-bit integers. At crypto.stackexchange.com I suggested to use 256-bit integers but it turns out you don't need so many bits to be almost certain to have all of them linearly independent on GF(2).
Based on simulations (see Figure 1 for details) 80 × 64 bits has approximately 1 : 280 - 63.8 = 1 : 216.2 → 1 : 104.877 probability of having non-full rank. A random 64 × 64 matrix has a non-full rank with a probability of about 71.1%. Each additional bit drops this by 50%. The simplest way to generate this pool of random integers is to flip n coins 64 · 80 / n times, as you get 1 bit of randomness / coin / toss. This table needs to be published and/or communicated to the 2nd party in advance and can be used multiple times. Numbers are identified as r0 , r1 , ..., r63.
Commitment to a yes/no answer and be encoded as the parity of a binary integer v = 2i0 + 2i1 + ... + 2in (where ij-1 < ij). It is suggested to generate first 63 bits by random and choose the final bit according to the desired commitment. Then calculate the 80-bit "committed value" c = ri0 ⊕ ri1 ⊕ ... ⊕ rin, which is communicated to the 2nd party.
Calculating the commitment value c from from a m-bit input value v is O(m) operation, but recovering v from c is O(m3) effort. Thus with sufficiently large m it takes "too much" effort to reverse the process without access to a programmable calculator. However it is trivial to do on any phone or laptop.
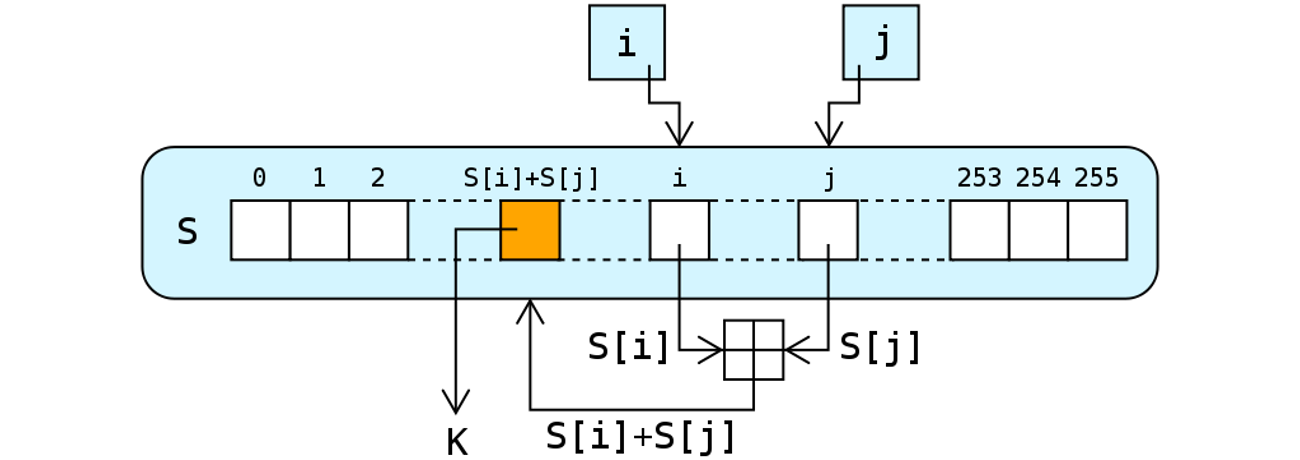
An alternative scheme is based on the well-known (and seriously flawed) RC4 stream cipher. On a setting with no access to a computer it should be sufficient to use less than 256 × 8 bits of state. As little as 32 or 64 integers could be sufficient against an attacker who does not possess a calculator, but I have no clue how to evaluate this.
The algorithm itself is well-described on Wikipedia and its operations are shown in Figure 2. It is a bit of an open question what is the best way of seeding the initial state, how many of the initial bits to skip and how many bits of output is needed for given security criteria. A simple solution is to use the standard key-scheduling algorithm, discard first 3 · n output bits (n being the number of internal state numbers) and then keeping the desired amount of output (like 80 or 128 bits) as the committed value. Even with all the flaws of RC4-based hashing, without access to an computer it should be difficult to recover the used key from this algorithm's output.
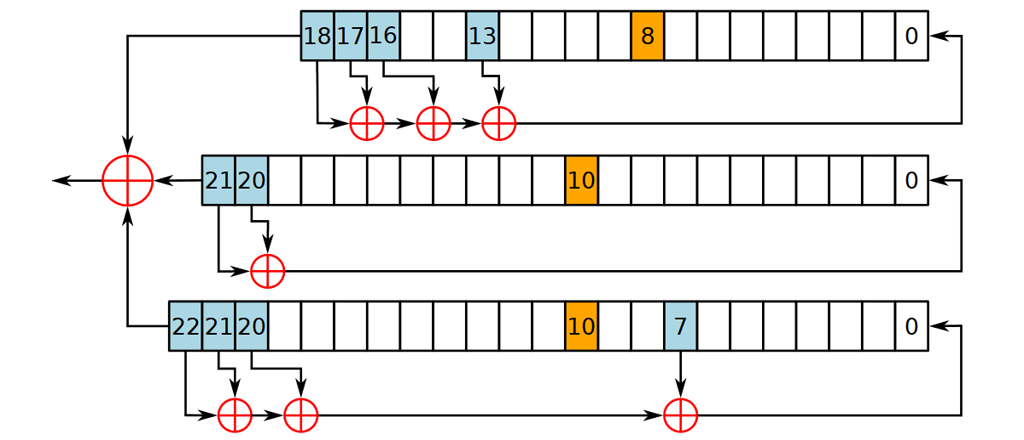
The final proposed algorithm is similar to RC4: A5/1 which used to encrypt GMS traffic. It has 19 + 22 + 23 = 64 bits of state, so you'd actually just need 64 coins to represent the state (heads vs. tails). It consist of only simple operations but they are quite verbose to execute manually. Suggested protocol is to commit to an initial state, skip first 64 - 192 bits and publish next 80 bits as the committed value. Again it should be difficult to recover the initial state by only observing this output.
Related blog posts:
|
|
|
|
|
|
|
|